Вся электронная библиотека >>>

Экология и безопасность жизнедеятельности >>

 

9.4. Матричные модели

 

Матричную модель можно рассматривать как конечно-разностный аналог динамической модели. Один из ранних вариантов матричной модели был разработан Льюисом и Лесли [30] как детерминистская модель, предсказывающая будущую возрастную структуру популяции самок по известной структуре в настоящий момент времени и гипотетическим коэффициентам выживания и плодовитости. Популяцию разбивают на n+1 возрастную группу (т. е. 0, 1, 2,..., п, причем каждая группа состоит из особей одного возраста), так что самая старшая группа, или группа, в которой все доживающие до данного возраста животные вымирают, имеет номер п. Обозначая через x_n число особей в каждой возрастной группе, получаем вектор  представляющий возрастную структуру в момент времени t.

Модель описывается матричным уравнением

                (9.19)

которое запишем в развернутом виде:

где величины f_i,(i=0,1,...,n) представляют число самок, производимых самкой i-го возраста,

р, (i = 0,1,..., п -1) – вероятность того, что самка i-го возраста доживет до возраста i+1.

Покажем, что поведение модели можно предсказать, анализируя некоторые формальные свойства матрицы А. Во-первых, последовательно умножая уравнение (9.19) на матрицу А, легко получить более общие уравнения для численности возрастных групп к моменту времени

                        (9.21)

Во-вторых, поскольку матрица А квадратная с (n+1) строками и столбцами, она имеет n+1 собственных чисел (с учетом кратности) и (n+1) собственных (и присоединенных) векторов. Элементы А являются либо положительными числами, либо нулями, поэтому наибольшее (по абсолютной величине) собственное число и координаты отвечающего ему собственного вектора положительны и при этом имеют определенный экологический смысл. Проиллюстрируем это на одной из простейших моделей, предложенных Уильямсоном [54].

Исходная популяция имеет вектор, представляющий возрастную структуру а₀ = (0,0,1), т. е. популяция состоит из одной самки старшего возраста. Матрица А имеет вид:

По прошествии одного временного интервала имеем

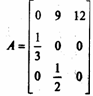
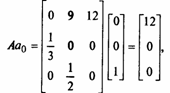
т. е. a₁ = (12, 0, 0) и в популяции уже будет 12 самок младшего возраста. Повторное применение модели дает следующие результаты:

и т.д.

Главное собственное число и собственный вектор матрицы А можно найти известными методами, имея

                     (9.22)

или полагая  – систему линейных алгебраических уравнений

определитель которой

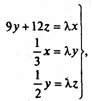
Следовательно, главное собственное число λ₁ = 2 и собственный вектор в силу (9.23) имеет вид  = (24, 4,1). Остальные собственные числа в силу (9.24) имеют вид λ₂ =-1, λ₃ =-1. В силу (9.23) собственный вектор  имеет вид = (6,-2,1). Так как собственное число -1 двукратно, то для нахождения вектора  (называемого присоединенным), решаем систему уравнений (A- λ₂) =:

 

(9.25)

 

Нетрудно проверить, что система (9.25) допускает решение  = (0, - 2, 2). Привлекая геометрические соображения, заключаем, что возрастная структура популяции представляется вектором в трехмерном пространстве, в котором векторы  = (24,4, 2),  = (6, - 2,1) и = (0, - 2, 2) – базисные, т. е.

                  (9.26)

где α₀, β₀, γ₀ – некоторые положительные числа (например, если  = (258, 30, 17), то α₀=10, β₀=3, γ₀=2).

Тогда уравнение (9.21) примет вид:

 (9.27)

Так как → 0, k → ∞, то при t=+k → ∞  популяция возрастает по экспоненциальному закону

 (9.28)

Главное собственное число λ₁ дает скорость, с которой возрастает размер популяции (в нашем примере за каждый временной интервал популяция удваивается), а собственный вектор  определяет устойчивую возрастную структуру популяции, т. е. отношение численностей особей разных возрастных групп остается постоянным и равным 24:4:1. Нетрудно видеть, что если мы в конце каждого временного интервала будем изымать половину популяции и использовать на корм, то размер ее станет равным исходному .

Матричные модели очень удобны для расчета на ЭВМ и находят все более широкое применение, например, для анализа круговорота питательных веществ в экосистемах, в различных стохастических моделях [54] (в марковских моделях и т.д.).

 

К содержанию книги:  Экология и безопасность жизнедеятельности

 

Смотрите также:

 

Экологическое право. Вопросы и аспекты  "Экологическое право. Право окружающей среды"   "Экологическое право"   "Экологическое право" 

 

Цены и ценообразование   Цены и ценообразование  "Финансовое право"   "Хозяйственное право"

 

ЭКОЛОГИЯ — наука, изучающая условия существования живых организмов ...

Впервые термин «экология» был использован нем. биологом Э. Геккелем в 1866 г., однако наиболее активное развитие Э. началось лишь в 30-х гг. 20 в. ... www.bibliotekar.ru/624-7/67.htm

 

Экономические основы решения экологического, сырьевого и ...

На уже функционирующие международные и региональные экологические организации ... Экология в последнее время стала постоянным объектом. ... www.bibliotekar.ru/biznes-38/87.htm

 

Влияние урбанизированной жилой среды на условия проживания и ...

Рассмотрение экологических проблем с современных позиций позволяет утверждать, что ухудшение окружающей природной среды не является... www.bibliotekar.ru/zhilishe/2.htm

 

Оценка общей экономической ценности природных территорий

Экологические системы и особо охраняемые природные территории .... с определением хозяйственной и экологической ценности природных ресурсов. ... www.bibliotekar.ru/biznes-8/85.htm