|
Учебные пособия |
|
Моделирование рисковых ситуаций в экономике и бизнесе Раздел: Экономика |
4.2. ИЗМЕРЕНИЕ ОТНОШЕНИЯ К РИСКУ
Исследуем график функции полезности, представленной на рис. 4.4. Для такого типа ЛПР полезность среднего выигрыша (полезность ОДО) больше ожидаемой полезности игры: с вероятностью p выиграть М1 и с вероятностью (1 - р) выиграть М2.
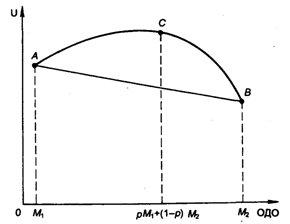
Рис. 4.4. График функции полезности ЛПР, не склонного к риску
Формально мы имеем график вогнутой функции, о которой известно, что ордината любой точки кривой больше ординаты точки хорды кривой. Определим соотношение, характеризующее ЛПР, не склонного к риску. Нетрудно видеть, что
U(M1) - значение полезности в точке А;
U(M2) - значение полезности в точке В;
U(pM1 + (1 - р)М2) - значение полезности в точке С.
Уравнение хорды АВ имеет вид:
U1 = а + bМ ,
где U1 - совокупность точек, лежащих на отрезке прямой.
Найдем значения параметров а и b уравнения прямой.
В точке А имеем U(M1) = а + bМ1.
В точке В имеем U(M2) = а + bМ2.
Вычитаем из первого выражения второе, исключая величину a:
U(M1) – U(M2) = b(M1 – М2) ,
откуда получаем:
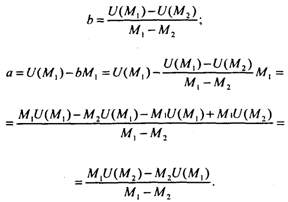
После подстановки значений для параметров а и b уравнение хорды АВ имеет вид:
![]()
где М1 £ М £ M2.
Пусть М = рМ1 + (1 – р)М2, где 0 £ р £ 1, тогда в точке С справедливо неравенство
![]()
Подставив в это неравенство вычисленные значения а и b, получим:
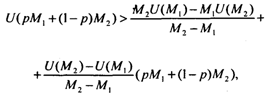
или
U(pM1 + (1 - р)М2) > PU(M1) + (1 - p)U(M2). (4.2)
Неравенство (4.2) характерно для функции полезности ЛПР, не склонных к риску. Оно действительно показывает, что полезность среднего выигрыша (полезность ОДО) больше ожидаемой полезности игры: с вероятностью р выиграть М1 и с вероятностью (1 – р) выиграть М2.
Аналогично можно показать, что для функций полезности ЛПР, склонных к риску, справедливо неравенство
U(pM1 + (1 – р)М2) < pU(M1) + (1 – p)U(M2). (4.3)
Для функций полезности ЛПР, безразличных (нейтральных) к риску, имеет место равенство
U(pM1 + (1 – р)М2) = pU(M1) + (1 – p)U(M2). (4.4)
Склонность или несклонность ЛПР к риску, как уже отмечалось, зависит от его финансового положения, текущей ситуации принятия решения и других факторов. Иначе говоря, эта характеристика ЛПР не является абсолютной, присущей ему при любых обстоятельствах.
Приведем пример игры, по отношению к которой любой игрок не склонен к риску.
Петербургский парадокс (игра придумана петербургскими гусарами). Играют двое. Один бросает монету до тех пор, пока не выпадет «орел». Выигрыш равен (2)n руб., где п - число бросков до появления «орла». Ожидаемая величина выигрыша:
ОДО = 2(1/2) + (2)2 (1/4) + (2)3(1/8) + ... = 1+1+1+ ... .
Вряд ли какой-либо игрок согласится заплатить за право участвовать в этой игре сумму, равную ОДО: эта сумма бесконечно велика.
Предположим теперь, что имеет место игра (лотерея) с альтернативами a и в, т.е. G(a,в: a). Исследуем проблему, как целесообразнее поступить ЛПР: играть или получить гарантированный выигрыш, равный ожидаемому выигрышу. Пусть функция полезности игрока определена как U(W) = ln(W), где W- величина благосостояния. Пусть игра заключается в выигрыше 5 дол. с вероятностью 0,8 и в выигрыше 30 дол. с вероятностью 0,2. Ожидаемая величина выигрыша (ОДО):
E(W) = 5*0,8 + 30*0,2 = 10 дол.
Для указанной логарифмической функции полезности имеем зависимость, выраженную в табл. 4.1.
Таблица 4.1
|
W |
1 |
5 |
10 |
20 |
30 |
|
U(W) |
0 |
1,61 |
2,30 |
3,00 |
3,40 |
Рассчитаем полезность ОДО для данной игры:
U(E(W)) = U(10) = ln(10) = 2,3,
т.е. полезность отказа от игры при получении гарантированного выигрыша, равного 10 дол. (ОДО данной игры), оценивается в 2,3 ютиля (ютиль - условная единица полезности). Если ЛПР предпочтет игру, то
E(U(W)) = 0,8U(5) + 0,2U(30) = 0,8*1,61 + 0,2*3,40 = 1,97 ютиля.
Для рассмотренной логарифмической функции полезности большей полезностью обладает вариант с получением гарантированного выигрыша, равного E(W)=ОДО, а не участие в игре (2,3 > 1,97). Такое лицо, принимающее решение, не склонно к риску.
Выводы. Из соотношении (4.2) – (4.4) вытекает:
• если U(E(W)) > E(U(W)), игрок не склонен к риску;
• если U(E(W)) = E(U(W)), игрок нейтрален (безразличен) к риску;
• если U(E(W)) < E(U(W}), игрок склонен к риску.
Здесь Е и U - соответственно символы математического ожидания и функции полезности.
К содержанию книги: Моделирование рисковых ситуаций в экономике и бизнесе
Смотрите также:
ПРЕДПРИНИМАТЕЛЬСКИЙ РИСК предпринимательская ...
|
Такие предприниматели готовы рисковать, в рисковой
ситуации они |
Риск-менеджмент. Организация риск-менеджмента
|
Одна и та же рисковая ситуация воспринимается
разными людьми по- |
СТРАХОВАНИЕ. Организационная структура страхования
|
Страхование как экономическая категория включает
следующие элементы: |
Риск-менеджмент - часть финансового менеджмента
|
Объектом управления в риск-менеджменте являются
риск, рисковые |
Потребность делать нечто лучше, чем оно было сделано вчера ...
|
В отличие от менеджера, для предпринимателя поиск
рисковых ситуаций и |
КЛАССИФИКАЦИЯ ПРЕДПРИНИМАТЕЛЬСКИХ РИСКОВ С ...
|
С риском предприниматель сталкивается на разных
этапах своей |
Расчетно-кассовое обслуживание населения. Чековая книжка ...
|
В магазин не надо везти крупные суммы денег и
покупатель избавлен от |
Транснациональная корпорация (ТНК) представляет собой ...
|
... системы, коммунальные услуги; экономические и
финансовые условия; |
Управление риском. Понятие и виды экономических рисков ...
|
«Ситуация риска» отличается от «ситуации
неопределенности». ... Эти |
Политика доходов и заработной платы
Разработка управленческого решения
Исследование систем управления