Вся электронная библиотека >>>

Моделирование рисковых ситуаций  >>

 

4.3. СТРАХОВАНИЕ ОТ РИСКА

 

Пусть по-прежнему полезность выражается логарифмической зависимостью U(W) = ln(W) (см. табл. 4.1).

Определим, какую максимальную сумму пожелает заплатить ЛПР, чтобы избежать игры, в которой с вероятностью 0,8 он выигрывает 5 дол. (уменьшение выигрыша на 5 дол. по сравне­нию с ОДО = 10 дол.) и с вероятностью 0,2 выигрывает 30 дол. (увеличение выигрыша на 20 дол. по сравнению с ОДО). Значение ожидаемой полезности игры составляет 1,97 ютиля, что соответствует гарантированному выигрышу 7,17 дол. (ln7,17 = 1,97). С другой стороны, сумма ожидаемого выигрыша в случае игры (ОДО) равна 10 дол. Поэтому, чтобы избежать игры, ЛПР согласится заплатить максимальную сумму, равную

10 – 7,17 = 2,83 дол.

Из этого следует, что, если ЛПР предлагают застраховаться от игры и просят за это сумму, меньшую, чем 2,83 дол., ему выгодно принять предложение. В данном случае величина, рав­ная 2,83 дол., - премия (максимальная плата) за риск.

Рассмотрим некоторые приложения теории полезности.

Задача 4.2. Оптимальная величина страхования. Ювелир вла­деет бриллиантом стоимостью 100 000 дол. и желает застраховать его от кражи. Страховка покупается по правилу: цена страховки составляет 20 % от суммы, которую страхуют. Например, если бриллиант страхуется на всю стоимость (100 000 дол.), страховка стоит 20 000 дол., если страхуется на половину цены (50 000 дол.). то страховка обходится в 10 000 дол. Если ювелир будет знать (построит) свою функцию полезности, он сможет рассчитать, на какую оптимальную сумму следует застраховать дорогую вещь.

Ювелир может оказаться в одной из двух ситуации: 1) бриллиант украден; 2) бриллиант не украден. Чем больше сумма страхования, тем больше его состояние (капитал), если бриллиант украден, но тем меньше его состояние, если брил­лиант не украден.

Например, если бриллиант застрахован на 50 000 дол., име­ют место два случая:

1. Бриллиант украден. При этом потери ювелира рассчитыва­ются следующим образом:

-100 000 (бриллиант) - 10 000 (страховка) + 50 000 (компен­сация) = -60 000 дол., а капитал 50 000-10 000 = 40 000 дол.

2. Бриллиант не украден. В этом случае капитал ювелира составит:

100 000 (бриллиант) - 10 000 (страховка) = 90 000 дол.

Если бриллиант застрахован на 100 000 дол., то в случае кражи бриллианта капитал составит 100 000 - 20 000 = 80 000 дол. Если бриллиант не украден, капитал также составит 80 000 дол. Обозначим капитал ювелира в случае, если бриллиант не украден, через Y_n:

Y_n  = 100 000 - 0,2К,                                                              (4.5)

где К - сумма страхования.

 

 

Если бриллиант украден, то капитал ювелира определим как Y_t:

Y_t = 0,8 K .

Соответствующий график, отражающий бюджетное ограни­чение, представлен на рис. 4.5.

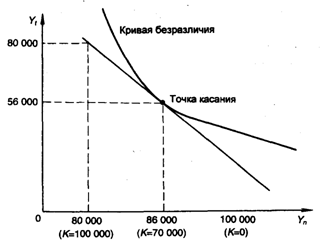
Рис. 4.5. Графическое решение задачи 4.2

Предположим, что можно экспертно определить вероятность р того, что бриллиант будет украден. Тогда полезность капитала Y_t, равна U(Y_t). Вероятность того, что бриллиант не украден, со­ставляет (1-р), и U(Y_n) - полезность капитала Y_n в этом случае.

Ожидаемая полезность U «игры» (с вероятностью р брилли­ант украден и с вероятностью (1 - р) - не украден) определяется согласно формуле (4.1) выражением

U = pU(Y_t)+(1-p)U(Y_n).

Значения Y_t  и Y_n следует выбирать таким образом, чтобы ожидаемая полезность была максимальной, т.е.

pU(Y_t) + (1-р)(Y_n)  max .

Пусть точка касания кривой безразличия (линия одинаковой полезности) на рис. 4.5 соответствует Y_n = 86 000 дол., Y_t = 56 000 дол.

Тогда согласно формуле (4.5) имеем: 86 000 = 100 000 - 0,2К, откуда оптимальная величина страхования К = 70 000 дол.

Задача 4.3. Спрос на страхование. Пусть финансовое состо­яние индивида оценивается заданным значением W. Предполага­ется, что можно вычислить вероятность р потери некоторой ча­сти этого состояния, определяемой суммой L £ W (например, в результате пожара). Индивид может купить страховой полис, в соответствии с которым ему возместят нанесенный ущерб в размере q. Плата за страхование составляет pq, где p - доля страхования в объеме нанесенного ущерба. Проблема состоит в определении значения q.

Исследуем задачу максимизации ожидаемой полезности фи­нансового состояния индивида в ситуации, когда с вероятностью р страховой случай происходит и с вероятностью (1 –р) - не происходит. Тогда задача сводится к поиску максимума по q ожидаемой полезности капитала индивида:

Применим необходимое условие оптимальности - продиффе­ренцируем выражение в квадратных скобках по q и приравняем производную нулю:

                                     

где q* - оптимальное значение q. В результате получаем:

                                         

Предполагая известным вид функции U, из соотношения (4.6) находим значение q*.

Рассчитаем ожидаемую прибыль страховой компании, учи­тывая, что страховой случай имеет вероятностный характер.

Если страховой случай произошел, компания получает доход pq – q. Если страховой случай не наступил, компания получает доход pq. Поэтому ожидаемая прибыль компании

р(pq - q)+ (1 - р) pq = ppq - pq + pq - ppq = q(p - р),

где р - вероятность наступления страхового случая.

Конкуренция между страховыми компаниями уменьшает прибыль, которая в условиях совершенной конкуренции стремит­ся к нулю, т.е. из условия q(p - р) = 0 следует, что p  р.

Это означает, что доля платежа от страхуемой суммы p при­ближается к вероятности несчастного случая р. Если соотноше­ние p = р ввести в условие максимума ожидаемой полезности, то получим:

.

Если потребитель не склонен к риску, то , и из равенства первых производных следует равенство аргументов, т.е.

W – L + (1 - p)q* =W – pq*,

или

– L + q* – pq* = –pq*,

откуда

q* = L.

Вывод. Страховаться целесообразно на сумму, которую мож­но потерять в результате несчастного случая.

 

К содержанию книги:   Моделирование рисковых ситуаций в экономике и бизнесе

 

Смотрите также:

 

    ПРЕДПРИНИМАТЕЛЬСКИЙ РИСК предпринимательская ...

Такие предприниматели готовы рисковать, в рисковой ситуации они маневрируют ресурсами, способны очень быстро находить новых партнеров bibliotekar.ru/biznes-41/29.htm

 

  Риск-менеджмент. Организация риск-менеджмента

Одна и та же рисковая ситуация воспринимается разными людьми по- разному. Поэтому оценка риска и выбор финансового решения во многом ... bibliotekar.ru/finance-2/102.htm

 

  СТРАХОВАНИЕ. Организационная структура страхования

Страхование как экономическая категория включает следующие элементы: рисковые обстоятельства, ситуация риска, стоимость (оценка) объекта ... bibliotekar.ru/risk-menedgment/7.htm

 

  Риск-менеджмент - часть финансового менеджмента

Объектом управления в риск-менеджменте являются риск, рисковые вложения .... При отсутствии типовых ситуаций финансовый менеджер bibliotekar.ru/risk-menedgment/4.htm

 

  Потребность делать нечто лучше, чем оно было сделано вчера ...

В отличие от менеджера, для предпринимателя поиск рисковых ситуаций и умение их разрешать обладают самодостаточной ценностью. Только на ... bibliotekar.ru/menedzhment-2/195.htm

 

  КЛАССИФИКАЦИЯ ПРЕДПРИНИМАТЕЛЬСКИХ РИСКОВ С ...

С риском предприниматель сталкивается на разных этапах своей деятельности, и, естественно, причин возникновения рисковой ситуации ... bibliotekar.ru/biznes-41/30.htm

 

  Расчетно-кассовое обслуживание населения. Чековая книжка ...

В магазин не надо везти крупные суммы денег и покупатель избавлен от рисковых ситуаций в дороге. В свою очередь магазин освобождается от ... bibliotekar.ru/bank-4/36.htm

 

  Транснациональная корпорация (ТНК) представляет собой ...

... системы, коммунальные услуги; экономические и финансовые условия; восприятие культуры; рисковые ситуации, включая политический риск (рис. ... bibliotekar.ru/teoriya-organizacii/140.htm

 

  Управление риском. Понятие и виды экономических рисков ...

«Ситуация риска» отличается от «ситуации неопределенности». ... Эти мероприятия и составляют содержание рисковой политики. ... bibliotekar.ru/biznes-38/16.htm

Политика доходов и заработной платы 

 

Разработка управленческого решения

 

Исследование систем управления 

 

Организационное поведение и управление персоналом