|
Учебные пособия |
|
Моделирование рисковых ситуаций в экономике и бизнесе Раздел: Экономика |
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задача 4.4. Допустим, что функция полезности ЛПР логарифмическая U(W) = ln(W) и весь его капитал составляет 5 тыс. руб.
Возникают две ситуации:
1. С вероятностью 0,5 ЛПР может выиграть и проиграть 1 тыс. руб. Есть ли смысл покупать страховой полис, устраняющий риск, за 125 руб.?
2. ЛПР рискнул, отказался от страхового полиса и проиграл 1 тыс. руб. Та же ситуация возникла во второй раз. Следует ли ему застраховаться от риска на прежних условиях (125 руб. за страховой полис). Что целесообразнее: приобрести полис или принять участие в игре?
Задача 4.5. Предположим, что ваша функция полезности определяется логарифмической зависимостью U(W)=ln(W) и вы сталкиваетесь с ситуацией, когда можете с равными шансами выиграть и проиграть
1 тыс. руб. Сколько вы готовы заплатить, чтобы избежать риска, если текущий уровень вашего благосостояния равен 10 тыс. руб.? Сколько вы заплатили бы, если бы ваше состояние было 1 млн руб.?
Задача 4.6. Мелкий бизнесмен сталкивается с ситуацией, когда с вероятностью 10 % пожар может уничтожить все его имущество, с вероятностью 10 % - уменьшить его недвижимость до 50 тыс. руб., с вероятностью 80 % огонь не принесет ему вреда и стоимость его имущества останется равной 100 тыс. руб. Какую максимальную сумму он готов заплатить за страховку, если его функция полезности имеет логарифмический вид U(W) = ln(W), а страховые выплаты составляют 100 тыс. руб. для первого случая и 50 тыс. руб. для второго случая?
Задача 4.7. Пусть функция полезности «нового русского» имеет вид:
U(W) = 10 + 2W,
где W - денежный выигрыш.
Бизнесмен может вложить в строительство магазина 25 тыс. руб. и считает, что с вероятностью 0,5 он получит прибыль в 32 тыс. руб. и с вероятностью 0,5 потеряет весь свой капитал. Определите:
• Следует ли осуществлять инвестирование проекта?
• Если будет сделано инвестирование, то какова ожидаемая полезность этого мероприятия?
Задача 4.8. В профессиональном теннисе нередко имеет место практика дележа призов за первое и второе места поровну между финалистами (тайный сговор до начала состязания). Например, если первый приз равен 100 000 дол., а второй - 32 000 дол., то каждый получает по 66 000 дол. (66 000 = (100 000 + 32000) / 2). Определите:
• Если игрок склонен к риску и уверен, что его выигрыш и проигрыш равновероятны (50 %), то согласится ли он участвовать в дележе?
• Предположим, что функция полезности одного из игроков имеет вид, представленный на рис. 4.6. Пожелал бы такой игрок участвовать в дележе призов, если шанс выиграть составляет 50 %?
• Как правило, игроки, попавшие в финал, не соглашаются на предварительный дележ призов, поскольку они уверены в своей победе. Какова должна быть минимальная вероятность выигрыша, чтобы с представленной на рис. 4.6 функцией полезности рассчитывать на получение приза за первое место?
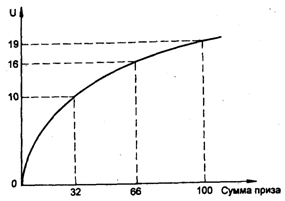
Рис. 4.6. Функция полезности одного из игроков в задаче 4.8
Задача 4.9. Предполагается, что типичная функция полезности дохода для человека имеет вид, показанный на рис. 4.7. Определите:
• Предпочтет ли такой человек получить со 100 %-ной определенностью доход В или принять участие в игре, в которой с вероятностью 0,5 получает доход А и с вероятностью 0,5 - доход С, где В = А/2 + С/2?
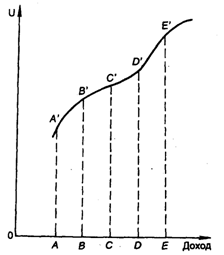
Рис. 4.7. Типичная функция полезности дохода для человека
• Предпочтет ли человек с такой функцией полезности получить со 100 %-нои определенностью доход D или принять участие в игре, в которой выигрывает сумму С с вероятностью 0,5 и сумму Е с вероятностью 0,5 (D=C/2 + E/2)?
Задача 4.10. Управляющий банком во время своего отпуска желает совершить кругосветное путешествие, которое стоит 10 000 дол. Полезность путешествия можно оценить количеством денег, потраченных на отдых (W).
Пусть его функция полезности выражается зависимостью U(W) = ln(W). Определите:
• Если существует вероятность, равная 0,25, потерять во время путешествия 1 000 дол., то какова ожидаемая полезность кругосветного путешествия?
• Отдыхающий банкир может приобрести страховку от потери 1 000 дол. за 250 дол., купив, например, дорожные чеки. Покажите, что ожидаемая полезность в случае, когда он покупает страховку, выше по сравнению с ситуацией, когда потеря 1 000 дол. происходит без страхования.
• Какова максимальная денежная сумма, которую банкир готов заплатить за страховку от потери 1 000 дол.?
К содержанию книги: Моделирование рисковых ситуаций в экономике и бизнесе
Смотрите также:
ПРЕДПРИНИМАТЕЛЬСКИЙ РИСК предпринимательская ...
|
Такие предприниматели готовы рисковать, в рисковой
ситуации они |
Риск-менеджмент. Организация риск-менеджмента
|
Одна и та же рисковая ситуация воспринимается
разными людьми по- |
СТРАХОВАНИЕ. Организационная структура страхования
|
Страхование как экономическая категория включает
следующие элементы: |
Риск-менеджмент - часть финансового менеджмента
|
Объектом управления в риск-менеджменте являются
риск, рисковые |
Потребность делать нечто лучше, чем оно было сделано вчера ...
|
В отличие от менеджера, для предпринимателя поиск
рисковых ситуаций и |
КЛАССИФИКАЦИЯ ПРЕДПРИНИМАТЕЛЬСКИХ РИСКОВ С ...
|
С риском предприниматель сталкивается на разных
этапах своей |
Расчетно-кассовое обслуживание населения. Чековая книжка ...
|
В магазин не надо везти крупные суммы денег и
покупатель избавлен от |
Транснациональная корпорация (ТНК) представляет собой ...
|
... системы, коммунальные услуги; экономические и
финансовые условия; |
Управление риском. Понятие и виды экономических рисков ...
|
«Ситуация риска» отличается от «ситуации
неопределенности». ... Эти |
Политика доходов и заработной платы
Разработка управленческого решения
Исследование систем управления