|
Учебные пособия |
|
Моделирование рисковых ситуаций в экономике и бизнесе Раздел: Экономика |
6.1. ОБЩИЕ СВЕДЕНИЯ
Создателем теории статистических игр считается А. Вальд. Он показал, что в теории принятия решений статистические игры являются основным подходом, если решение принимается в условиях частичной неопределенности.
Статистические модели представляют собой игру двух лиц (человека и природы) с использованием человеком дополнительной статистической информации о состояниях природы.
Она существенно отличается от антагонистической игры двух лиц с нулевой суммой, где выигрыш одного равен проигрышу другого.
В статистической игре природа не является разумным игроком, который стремится выбрать для себя оптимальные стратегии. Этот игрок не заинтересован в выигрыше. Другое дело -человек, в данном случае статистик. Он имеет целью выиграть игру с воображаемым противником, т. е. с природой.
Игрок-природа не выбирает оптимальной стратегии, но статистик должен стремиться к определению распределения вероятностей состояния природы. Следовательно, основными отличиями статистической игры от стратегической являются:
• отсутствие стремления к выигрышу у игрока-природы, т. е. отсутствие антагонистического противника;
• возможность второго игрока - статистика провести статистический эксперимент для получения дополнительной информации о стратегиях природы.
Так, например, статистик, работающий в фирме «Одежда», может изучить многолетние данные о погодных условиях в местностях, где одежда будет продаваться, и в зависимости от наиболее вероятного состояния погоды выработать рекомендации, куда и какое количество партий изделий отправлять, где выгоднее и на каком уровне провести сезонное снижение цен и т. д.
Таким образом, теория статистических решений является теорией проведения статистических наблюдений, обработки этих наблюдений и их использования.
В теории статистических решений основные правила могут быть детерминированными и рандомизированными.
В статистических играх используются понятия: риск (функция риска), потери (функция потерь), решение (функция решения), функции распределения при определенных условиях.
Необходимо пояснить понятие рандомизации. Это статистическая процедура, в которой решение принимается случайным образом. Математическая энциклопедия это определяет более подробно: «Статистическая процедура принятия решения, в которой по наблюденной реализации х случайной величины Х решение принимается с помощью розыгрыша по вероятностному закону, называется рандомизацией»*.
* Математическая энциклопедия. Т.4. - М.: Советская энциклопедия, 1984. - С. 865.
Введем условные обозначения:
В или W - множество состояний природы;
В. или Qj - отдельное состояние природы, Qj Î W;
А — множество действий (решений) статистика;
а - отдельное решение статистика, a Î А;
L - функция потерь. Множества W и А предполагаются численно определенными, поэтому представляется возможным установить распределение вероятностей. Если принятое статистиком решение a Î А и состояние природы Q Î W, то функция потерь запишется L(Q; a);
D - совокупность всех нерандомизированных (чистых) функций решения;
d(![]() ) - функция
решения;
) - функция
решения; ![]() -
случайный вектор. Характеристикой функции решения является функция потерь.
Статистик может перед принятием одного из возможных решений провести
эксперимент, который заключается в наблюдении случайной переменной х. В
итоге представляется возможным получить распределение этой случайной
переменной в зависимости от состояния природы Q;
-
случайный вектор. Характеристикой функции решения является функция потерь.
Статистик может перед принятием одного из возможных решений провести
эксперимент, который заключается в наблюдении случайной переменной х. В
итоге представляется возможным получить распределение этой случайной
переменной в зависимости от состояния природы Q;
F(x|Q) - функция условного распределения случайной переменной х. Предполагается, что для каждого состояния природы Q известно значение функции F(x|Q);
п - объем выборки;
xQ —
множество всех выборок объема п. После получения результата
эксперимента х статистик использует некоторую функцию решения и
принимает одно из решений а Î А,
когда результат эксперимента - вектор ![]() :
:
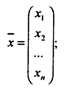
R — функция риска;
R(Q,d) - функция риска, определенная на прямом произведении W´D множества состояний природы и множества решений.
Игра (W, A, L) - исходная стратегическая игра, соответствующая стратегической задаче принятия решения;
G = (W, D, R) - статистическая игра;
s - рандомизированная функция решения;
D* - множество случайных функций решения, s Î D*. Подразумевается, что D Ì D*, так как чистая функция решения (нерандомизированная) может быть рассмотрена как смешанная, которая используется с вероятностью, равной 1;
G(Q) - функция априорного распределения состояний природы Q;
X - совокупность всех априорных распределений x Î X.
К содержанию книги: Моделирование рисковых ситуаций в экономике и бизнесе
Смотрите также:
ПРЕДПРИНИМАТЕЛЬСКИЙ РИСК предпринимательская ...
|
Такие предприниматели готовы рисковать, в рисковой
ситуации они |
Риск-менеджмент. Организация риск-менеджмента
|
Одна и та же рисковая ситуация воспринимается
разными людьми по- |
СТРАХОВАНИЕ. Организационная структура страхования
|
Страхование как экономическая категория включает
следующие элементы: |
Риск-менеджмент - часть финансового менеджмента
|
Объектом управления в риск-менеджменте являются
риск, рисковые |
Потребность делать нечто лучше, чем оно было сделано вчера ...
|
В отличие от менеджера, для предпринимателя поиск
рисковых ситуаций и |
КЛАССИФИКАЦИЯ ПРЕДПРИНИМАТЕЛЬСКИХ РИСКОВ С ...
|
С риском предприниматель сталкивается на разных
этапах своей |
Расчетно-кассовое обслуживание населения. Чековая книжка ...
|
В магазин не надо везти крупные суммы денег и
покупатель избавлен от |
Транснациональная корпорация (ТНК) представляет собой ...
|
... системы, коммунальные услуги; экономические и
финансовые условия; |
Управление риском. Понятие и виды экономических рисков ...
|
«Ситуация риска» отличается от «ситуации
неопределенности». ... Эти |
Политика доходов и заработной платы
Разработка управленческого решения
Исследование систем управления