|
Учебные пособия |
|
Моделирование рисковых ситуаций в экономике и бизнесе Раздел: Экономика |
6.2. СВОЙСТВА СТАТИСТИЧЕСКИХ ИГР
Функция решения, отображающая множество
выборок XQ в множество решений статистика A, называется нерандомизированной
(чистой) функцией решения статистика. Так, по результатам эксперимента 
статистик определяет,
какое решение а Î А
он должен выбрать. Для выбора из множества D наилучшей функции
решения он использует функцию риска.
Функция риска зависит от множества
состояний природы и от множества функций решения и принимает значение, выраженное
действительными числами. Она определяет математическое ожидание функции потерь
при некотором состоянии природы Q и
известной статистику функции распределения F(|Q), когда а=d().
Представим функцию риска:
,
где M - знак математического ожидания;
L(Q, a) - функция потерь при
состоянии природы Q и d()
= a.
В теории статистических функций любую неотрицательную функцию L, определенную прямым произведением W´D, называют функцией потерь. Значение L(Q,d) функции потерь L в произвольной точке (Q, d)Î W´D интерпретируют как ущерб, к которому приводит принятие решений d, dÎD, если истинное значение параметра есть Q, Q Î W.
Выражение W´D - прямое произведение множества состояний природы и множества функций решения. Функция R(Q, d) не является случайной величиной, а принимается как платеж статистика в его игре с природой при следующих условиях:
• состояние природы фиксировано;
• функция решений выбрана, d Î D.
Стратегическая игра (W, A, L) становится статистической, G
= (W,
D, R), если используется
результат эксперимента - вектор . Игра называется статистической, если в ней:
• XQ - множество n-мерных выборок;
• D - множество функций решений, которые преобразуют XQ в А;
• W - множество состояний природы;
• R(Q, d) - функция риска.
Статистическая игра записывается как G = (W, D, R). Данная игра является игрой двух лиц с нулевой суммой, где dÎD -функция решения статистика, а риск R(Q, d) статистика - платеж природе.
Статистик может не прибегать к рандомизации, если он использует как оптимальную байесовскую функцию решения r (см. разд. 6.2.1).
Рандомизация на стороне статистика проводится двумя методами:
1) применение решений аÎА с определенными вероятностями (смешение решений);
2) смешение чистых функций решения dÎD, т.е. рандомизация функций решения.
Чаще применяется второй метод.
Распределение вероятностей d на множестве D чистых функций решения d называется рандомизированной (смешанной) функцией решения статистика.
Функция риска становится случайной величиной, если экспериментатор применяет в статистической игре случайную функцию решения dÎD*, т. е. когда каждой чистой функции решения dÎD приписывается вероятность, с которой она должна использоваться.
Платежом будет математическое ожидание функции потерь, взятое для некоторого состояния природы Q при распределении d, определенном на множестве чистых функций решения D:
Если статистик использует случайные функции решения dÎD*, то этим расширяется (обобщается) статистическая игра.
Расширенная статистическая игра (W, D*, R) называется также смешанным расширением статистической игры с рандомизацией на стороне статистика.
Дальнейшее расширение статистической игры может быть достигнуто при предположении, что природа также «применяет» стратегию при «выборе» своего состояния Q.
Априорное распределение вероятностей x на множестве W состояний природы означает распределение до проведения эксперимента. Это априорное распределение xÎX состояний природы является случайной (смешанной) стратегией природы в статистической игре, где природа не рассматривается как разумный игрок.
Если Q предполагается случайной величиной с априорным распределением x, то риск R(Q,d) становится случайной переменной при фиксированной функции решения d. В данном случае математическое ожидание риска R(Q,d) при априорном распределении x, задаваемом функцией распределения G(Q), определяется как
,
где r(x,d) -байесовский риск функции решения d с учетом априорного распределения x.
Если в качестве оптимальной принимается байесовская функция решения, то используется формула r(x,d).
Вводя рандомизацию на стороне природы, приходим к дальнейшему расширению статистической игры.
Игра (X, D*, r) со смешанным расширением статистической игры с рандомизацией на стороне статистика и на стороне природы называется полностью расширенной статистической игрой.
Поясним в полностью расширенной статистической игре (X, D*, r) ее составляющие:
X - множество всех априорных распределений x состояний природы или множество ее смешанных стратегий;
D* - множество всех случайных функций решения;
r = r(x,d) - байесовский риск.
Представим схему расширения статистической игры (рис. 6.1). При наличии данных без учета стохастических распределений имеем исходную стратегическую игру двух лиц с нулевой суммой, которая относится к антагонистическим играм. Данная игра является исходной для соответствующей статистической задачи принятия решения.
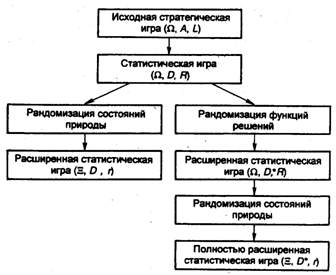
Рис. 6.1. Расширение статистической игры
Если статистик (экспериментатор) не имеет возможности провести эксперимент со случайной величиной X, чтобы получить ее распределение, которое зависит от состояния природы, он вынужден будет использовать только стратегическую игру (W, A, L).
Однако очень часто статистик может
провести эксперимент и получить в результате вектор , которым он в состоянии воспользоваться при
принятии решения аÎА
функции d(). В этом случае платеж L(Q, а)
становится случайной величиной, а игра - статистической G(W, D, R).
Стратегией статистика будет dÎD, а платежом природе от
статистика станет его риск R(Q, d).
Далее у статистика остаются две альтернативы:
1) воспользоваться рандомизацией состояний природы и перейти к расширенной (X, D, r) статистической игре;
2) воспользоваться рандомизацией функций решения и перейти к расширенной статистической игре (W, D*, R).
Наконец, если статистик применит смешанные стратегии для обоих игроков, то получит полностью расширенную статистическую игру ((W, D*, r).
На практике статистик для выбора оптимальной стратегии может не производить рандомизацию, а в качестве оптимальной взять байесовскую функцию решения.
А. Вальд, создавая теорию статистических игр, опирался на созданную Д. Нейманом теорию стратегических игр, поэтому сравним далее понятия стратегических игр двух лиц с нулевой суммой и понятия статистических игр статистика с природой. Для этого укажем основные обозначения в стратегической и статистической играх:
Х - совокупности стратегий игрока 1;
Y - совокупности стратегий игрока 2;
W— платежная функция;
W(X,Y) - платеж игрока 2 игроку 1;
G == (X,Y,W) - игра игрока 1 с игроком 2;
Г = (X, Н, К) ~ смешанное расширение игры G = (X, Y,W), где X - множество всех смешанных стратегий x игрока 1;
Н - множество всех смешанных стратегий h игрока 2;
К - риск игрока 2.
Составим сравнительную таблицу задач статистических решений с игрой двух лиц с нулевой суммой (табл. 6.1).
Таблица 6.1
К содержанию книги: Моделирование рисковых ситуаций в экономике и бизнесе
Смотрите также:
ПРЕДПРИНИМАТЕЛЬСКИЙ РИСК предпринимательская ...
|
Такие предприниматели готовы рисковать, в рисковой
ситуации они |
Риск-менеджмент. Организация риск-менеджмента
|
Одна и та же рисковая ситуация воспринимается
разными людьми по- |
СТРАХОВАНИЕ. Организационная структура страхования
|
Страхование как экономическая категория включает
следующие элементы: |
Риск-менеджмент - часть финансового менеджмента
|
Объектом управления в риск-менеджменте являются
риск, рисковые |
Потребность делать нечто лучше, чем оно было сделано вчера ...
|
В отличие от менеджера, для предпринимателя поиск
рисковых ситуаций и |
КЛАССИФИКАЦИЯ ПРЕДПРИНИМАТЕЛЬСКИХ РИСКОВ С ...
|
С риском предприниматель сталкивается на разных
этапах своей |
Расчетно-кассовое обслуживание населения. Чековая книжка ...
|
В магазин не надо везти крупные суммы денег и
покупатель избавлен от |
Транснациональная корпорация (ТНК) представляет собой ...
|
... системы, коммунальные услуги; экономические и
финансовые условия; |
Управление риском. Понятие и виды экономических рисков ...
|
«Ситуация риска» отличается от «ситуации
неопределенности». ... Эти |
Политика доходов и заработной платы
Разработка управленческого решения
Исследование систем управления