|
Учебные пособия |
|
Моделирование рисковых ситуаций в экономике и бизнесе Раздел: Экономика |
6.2.1. ВЫБОР ФУНКЦИЙ РЕШЕНИЯ
Для всех состояний природы не существует одной наилучшей функции решения. От статистика требуется применение таких методов, которые дают оптимальные функции решения в более узком диапазоне.
Для этого необходимо использовать критерии оптимальности.
Статистик в статистической игре (W, D, R) или в расширенных статистических играх стремится к выигрышу, т. е. к определению наилучшей функции решения, при которой риск R(Q, d) был бы минимальным. Но это не просто, так как для каждого состояния природы Q имеется своя лучшая функция.
Пусть у нас имеются две различные функции решения d1 и (рис. 6.2).
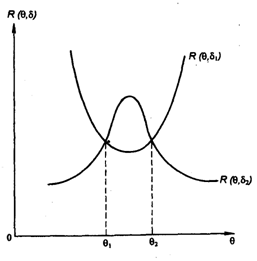
Рис. 6.2. Сравнение двух функций решения
Можно выделить область, где функция d1 будет лучшей, - в диапазоне состояний природы Q1< Q<Q2. Вторая функция d2 будет лучшей для состояния природы при Q<Q1 и при Q>Q2.
Функция d Î D называется допустимой, если в множестве D* нет никакой другой функции решения d0, которая была бы лучшей d для всех QÎW. Данная функция для каждого QÎW должна удовлетворять неравенству R(Q,d0) £ R(Q,d). Таким образом, допустимая функция решения не будет доминирующей стратегией статистика в статистической игре.
Рассмотрение только допустимых функций существенно уменьшит множество D* до множества допустимых функций решения.
Отметим, что байесовские функции решения входят в класс допустимых функций.
Определение. Функция решения d0ÎD* называется байесовской относительно априорного распределения xÎX состояний природы Q, если она минимизирует байесовский риск r(x, d) на множестве D*.
Таким образом, r(x, d) = ![]() r(x, d).
Приведем формулу Байеса. Прежде чем ее написать, обратимся к теореме о полной
вероятности [2, разд. 2.5, 2.6].
r(x, d).
Приведем формулу Байеса. Прежде чем ее написать, обратимся к теореме о полной
вероятности [2, разд. 2.5, 2.6].
Теорема. Если событие А может наступить только при условии появления одного из событий В1, В2, ...,Bn, образующих полную группу несовместных событий, то вероятность события А равна сумме произведений вероятностей каждого из событий В1, В2, ...,Bn на соответствующую условную вероятность события А:
![]()
где P(Bi) - вероятность события Bi;
Р(А|Вi) - условная вероятность события А в случае, если событие Вi уже произошло.
Формула Байеса используется тогда, когда событие А появляется совместно с каким-либо из полной группы несовместных событий В1, В2, ..., Bn . Событие А произошло, и требуется произвести количественную переоценку вероятностей событий В1, В2, ..., Bn. При этом известны вероятности Р(В1), Р(В2),..., Р(Bn) до опыта (априорные). Требуется определить вероятности после опыта (апостериорные).
Апостериорные вероятности представляют собой условные вероятности Р(В1|А), Р(В2|А) ,..., Р(Вn|А). Вероятность совместного наступления событий А с любым из этих событий Вj по теореме умножения равна:
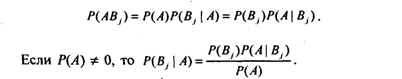
Эту формулу можно переписать исходя из формулы полной вероятности:
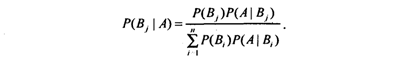
Задача 6.1. Собирается партия исправных изделий с трех предприятий. Первый завод поставляет 60 %, второй - 30 %, третий - 10 % изделий. В1, В2, В3 - события, соответствующие тому, что изделия изготовлены на первом, втором и третьем предприятиях.
Вероятность исправной работы изделий первого предприятия равна 0,98, второго - 0,99, третьего - 0,96.
Определить вероятность того, что в собранную партию исправных изделий попали соответственно изделия с первого, второго и третьего предприятий.
Введем обозначения:
А - событие, заключающееся в том, что изделие исправно;
Р(А) - полная вероятность того, что изделие исправно;
Р(В1|А), Р(В2|А), Р(В3|А) - условные вероятности того, что исправное изделие изготовлено соответственно на первом, втором и третьем предприятиях;
Р(A|В1), Р(A|В2), Р(A|В3) - условные вероятности того, что изделие, изготовленное соответственно на первом, втором и третьем предприятиях, исправно;
Р(В1), Р(В2), Р(В3) - вероятности того, что изделие изготовлено соответственно на первом, втором и третьем предприятиях.
Известно: Р(А|В1) = 0,98; Р(А|В2) = 0,99; Р(А|В3) = 0,96; Р(В1) = 0,60; Р(В2) = 0,30; Р(В3) = 0,10.
Требуется определить Р(А); Р(В1|А); Р(В2|А); Р(В3|А).
Решение. 1. Определим полную вероятность того, что изделия, прибывшие с разных предприятии, исправны:
![]()
2. Вычислим условные вероятности того, что в партию исправных попали изделия с первого, второго и третьего предприятии соответственно:

3. Проверим: Р(В1|А) + Р(В2|А) + Р(В3|А) = 0,599 + 0,303 + + 0,098 = 1.
Вывод. По формуле Байеса количественная переоценка доли предприятии в партии исправных изделии составляет: первое предприятие имеет 59,9 %; второе - 30,3 %; третье - 9,8 %.
Остановимся на некоторых нестандартных принципах принятия решений.
К содержанию книги: Моделирование рисковых ситуаций в экономике и бизнесе
Смотрите также:
ПРЕДПРИНИМАТЕЛЬСКИЙ РИСК предпринимательская ...
|
Такие предприниматели готовы рисковать, в рисковой
ситуации они |
Риск-менеджмент. Организация риск-менеджмента
|
Одна и та же рисковая ситуация воспринимается
разными людьми по- |
СТРАХОВАНИЕ. Организационная структура страхования
|
Страхование как экономическая категория включает
следующие элементы: |
Риск-менеджмент - часть финансового менеджмента
|
Объектом управления в риск-менеджменте являются
риск, рисковые |
Потребность делать нечто лучше, чем оно было сделано вчера ...
|
В отличие от менеджера, для предпринимателя поиск
рисковых ситуаций и |
КЛАССИФИКАЦИЯ ПРЕДПРИНИМАТЕЛЬСКИХ РИСКОВ С ...
|
С риском предприниматель сталкивается на разных
этапах своей |
Расчетно-кассовое обслуживание населения. Чековая книжка ...
|
В магазин не надо везти крупные суммы денег и
покупатель избавлен от |
Транснациональная корпорация (ТНК) представляет собой ...
|
... системы, коммунальные услуги; экономические и
финансовые условия; |
Управление риском. Понятие и виды экономических рисков ...
|
«Ситуация риска» отличается от «ситуации
неопределенности». ... Эти |
Политика доходов и заработной платы
Разработка управленческого решения
Исследование систем управления