Вся электронная библиотека >>>

Моделирование рисковых ситуаций  >>

 

8.4. ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО ЗАПАСА ПРОДУКЦИИ ТОРГОВОЙ ФИРМЫ НА ОСНОВЕ СТАТИСТИЧЕСКИХ ДАННЫХ

 

Пусть Q - рыночный спрос на продукт торговой фирмы для фиксированного периода (день, неделя, месяц). Воспримем это как спрос игрока 1. Этот спрос может быть любым действитель­ным положительным числом. Область состояний W = [0, ¥]. Про­даваемый продукт оценивается, например, в килограммах и мо­жет заказываться в любом количестве. Нереализованный в дан­ном периоде продукт не может быть продан в следующем пери­оде, так как теряет за время хранения свои потребительские качества. Значение QÎW заранее неизвестно.

Введем обозначения: а - запас продукта на некоторый пери­од. Следовательно, считаем, что множество решений фирмы А = [0, ¥]; аÎА - конкретное решение фирмы (игрока 2), при­нимаемое в статистической игре с природой, которая определяет действительный спрос Q на продукт; L(Q, a) - функция потерь. Она является функцией платежей в исходной стратегической игре (W, A, L); k₁ - себестоимость + дополнительные затраты на хра­нение 1 кг продукта, который не был продан в установленное время, так как спрос на него оказался меньше прогнозируемого;

k₂- потеря прибыли на 1 кг продукта, обусловленная отсутстви­ем товара, спрос на который превысил заказанное количество.

Принимая указанные обозначения, запишем кусочно-линей­ную функцию потерь фирмы:

 

Стратегическую игру (W, A, L) можно преобразовать в стати­стическую, если получить дополнительную статистическую ин­формацию о спросе на продукт QÎW. Действительный спрос по периодам представлен заказчиком. Это вектор

                                         

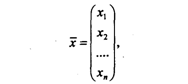
который в различные периоды времени представляет разные размеры спроса. Пусть а = d(x) - статистическая нерандомизи­рованная функция решения. Значение функции, определяющей оптимальное решение а об уровне запаса, найдем с помощью байесовской функции решения.

 

 

Известна функция действительного спроса на товар, соответ­ствующего статистическому наблюдению, т. е. .

Функцию априорного наблюдения G(Q|) распределения спро­са (состояний природы) обозначим F(Q).

Имеет место теорема: «Если, решая задачу, поставленную в форме статистической игры, статистик (игрок 2) провел экспе­римент, наблюдая случайную величину Х с функцией условного распределения G(Q|) или [F(Q)], и получил результат х, то не­случайная байесовская функция решения относительно некото­рого априорного распределения x состояний природы равна а = d(x), где а Î А - решение, минимизирующее ожидаемое зна­чение функции потерь L(Q, а) в условном апостериорном рас­пределении состояний природы, заданном функцией распреде­ления G(Q| x)».

Согласно данной теореме нужно минимизировать математи­ческое ожидание

                              

С использованием формулы (8.1) можно определить матема­тическое ожидание при апостериорном распределении спроса Q:

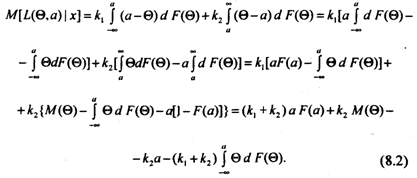
Минимизируя математическое ожидание функции потерь (8.2) относительно о, получим:

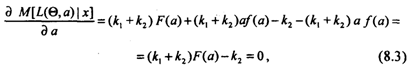
где f(a) - плотность в точке а апостериорного распределения спроса. В соответствии с необходимым условием (8.3) получим урав­нение

откуда

                                         

 

Итак, с помощью байесовской функции получено выражение для оптимального запаса. Оно равно числу а₀, удовлетворяюще­му равенству

где F(a₀) -функция апостериорного распределения спроса Q на про­дукт.

Результат (8.4) с учетом (8.5) означает, что для a₀ в распределении спроса Q должно выполняться условие . Значит, a₀ должно быть квантилем порядка  апостериорного распределения спроса Q.

Для вычисления оптимального запаса а₀ данного продукта на определенный период времени нужно:

1. Знать параметры k₁ и k₂, входящие в функцию потерь L(Q, a).

2. На основе статистических наблюдений получить апосте­риорное распределение спроса на товар.

3. С помощью функции этого распределения определить квантиль порядка .

Если, в частности, k₁ = k₂, то оптимальный уровень запаса a₀ будет соответствовать равенству F(a₀) = . Другими словами, оп­тимальный уровень запаса представляет собой медиану в апос­териорном распределении спроса Q.

Распределение близко к нормальному N(M, d), где М - мате­матическое ожидание, d - среднее квадратичное отклонение.

Значение a₀ (или квантиль порядка ) можно определить по таблице нормированного нормального распределения.

Иногда распределение не относится ни к одному из извест­ных исследователю законов распределения, тогда с помощью графика функции распределения спроса нужно определить квантиль порядка . Рассмотрим, как это делается на практике.

Пример 8.6. Требуется определить оптимальное значение за­паса товара. Известно: k₁ = 0,8; k₂ = 0,2; распределение спроса Q.

Решение. Представим распределение дневного спроса на товар, полученное по данным наблюдения (табл. 8.11).

Таблица 8.11

 

По табл. 8.11 строим график распределения спроса на товар (рис. 8.3).

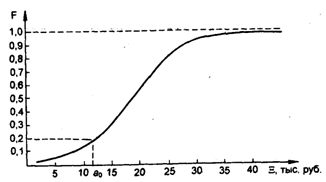
Рис. 8.3. Определение квантиля распределения

Рассчитаем квантиль распределения:

По квантилю, равному 0,2 (см. рис. 8.3), определяем a₀ = 12,3 тыс. руб. Это стоимостное выражение искомого оптимального запаса продукции торговой фирмы, равное 12,3 тыс. руб.

 

К содержанию книги:   Моделирование рисковых ситуаций в экономике и бизнесе

 

Смотрите также:

 

    ПРЕДПРИНИМАТЕЛЬСКИЙ РИСК предпринимательская ...

Такие предприниматели готовы рисковать, в рисковой ситуации они маневрируют ресурсами, способны очень быстро находить новых партнеров bibliotekar.ru/biznes-41/29.htm

 

  Риск-менеджмент. Организация риск-менеджмента

Одна и та же рисковая ситуация воспринимается разными людьми по- разному. Поэтому оценка риска и выбор финансового решения во многом ... bibliotekar.ru/finance-2/102.htm

 

  СТРАХОВАНИЕ. Организационная структура страхования

Страхование как экономическая категория включает следующие элементы: рисковые обстоятельства, ситуация риска, стоимость (оценка) объекта ... bibliotekar.ru/risk-menedgment/7.htm

 

  Риск-менеджмент - часть финансового менеджмента

Объектом управления в риск-менеджменте являются риск, рисковые вложения .... При отсутствии типовых ситуаций финансовый менеджер bibliotekar.ru/risk-menedgment/4.htm

 

  Потребность делать нечто лучше, чем оно было сделано вчера ...

В отличие от менеджера, для предпринимателя поиск рисковых ситуаций и умение их разрешать обладают самодостаточной ценностью. Только на ... bibliotekar.ru/menedzhment-2/195.htm

 

  КЛАССИФИКАЦИЯ ПРЕДПРИНИМАТЕЛЬСКИХ РИСКОВ С ...

С риском предприниматель сталкивается на разных этапах своей деятельности, и, естественно, причин возникновения рисковой ситуации ... bibliotekar.ru/biznes-41/30.htm

 

  Расчетно-кассовое обслуживание населения. Чековая книжка ...

В магазин не надо везти крупные суммы денег и покупатель избавлен от рисковых ситуаций в дороге. В свою очередь магазин освобождается от ... bibliotekar.ru/bank-4/36.htm

 

  Транснациональная корпорация (ТНК) представляет собой ...

... системы, коммунальные услуги; экономические и финансовые условия; восприятие культуры; рисковые ситуации, включая политический риск (рис. ... bibliotekar.ru/teoriya-organizacii/140.htm

 

  Управление риском. Понятие и виды экономических рисков ...

«Ситуация риска» отличается от «ситуации неопределенности». ... Эти мероприятия и составляют содержание рисковой политики. ... bibliotekar.ru/biznes-38/16.htm

Политика доходов и заработной платы 

 

Разработка управленческого решения

 

Исследование систем управления 

 

Организационное поведение и управление персоналом